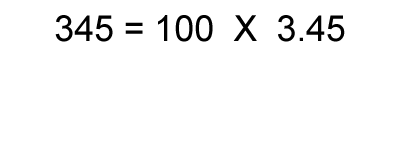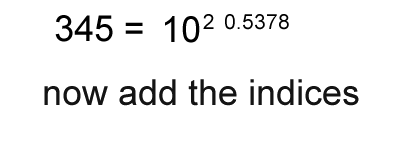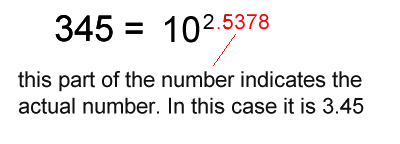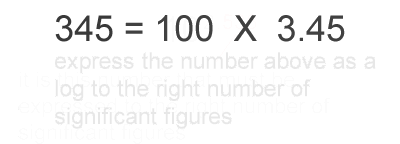
1. Calculate the logarithm of the number.
2. Round the result to keep the same number of decimal places as there were significant
figures in the original number.
Examples:
log(6.456×10³) = 3.809964 = 3.8100 (4 significant figures hence 4 decimal places)

The rules for expressing significant figures with logarithms will only rarely be encountered in chemistry. The main context for this rule will be the calculation of pH, during in acid-base chemistry.

Lets see some examples.

Calculate the pH of a 0.0452 M HCl.
=> The [H₃O⁺ ] = 0.0452
=> pH = -log^0.0452 = 1.34486
=> since [H₃O⁺ ] is expressed to three significant figures we must have three decimal places in the answer
=> pH = 1.345

A solution has a [H₃O⁺ ] = 0.003189 M. What is the pH of the solution?

=> The [H₃O⁺ ] = 0.003189
=> pH = -log^0.003189 = 2.496345
=> since [H₃O⁺ ] is expressed to four significant figures we must have four decimal places in the answer
=> pH = 2.4963

A solution has a [H₃O⁺ ] = 0.00032 M. What is the pH of the solution?

=> The [H₃O⁺ ] = 0.00032
=> pH = -log^0.00032 = 3.49485
=> since [H₃O⁺ ] is expressed to two significant figures we must have two decimal places in the answer
=> pH = 3.49