Buoyancy further exercises
The Bermuda Triangle has long been a fascination with people who believe that un-natural forces are acting in this region in order to explain the many disappearances of shipping vessels. One plausible theory involves the escape of huge quantities of natural gas. Gas deposits exist deep beneath the bottom of the sea. Occasionally huge amounts of methane escape creating giant air bubbles that surface underneath vessels. Explain with reference to buoyancy how a vessel can sink under such conditions.

 

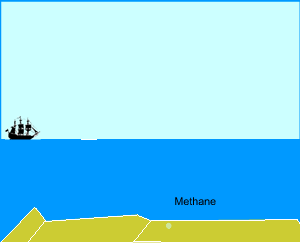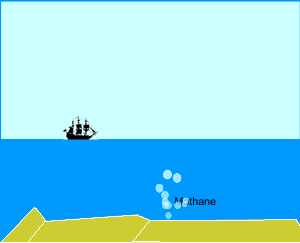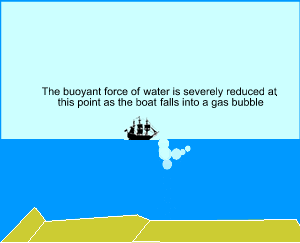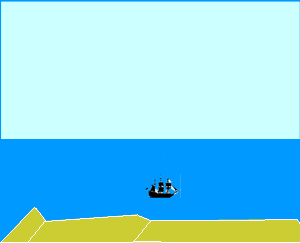
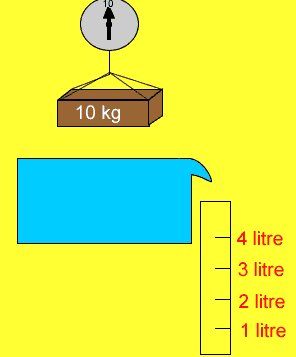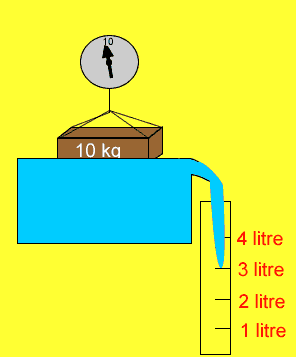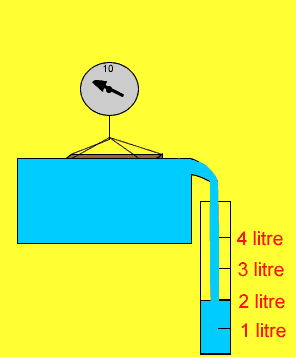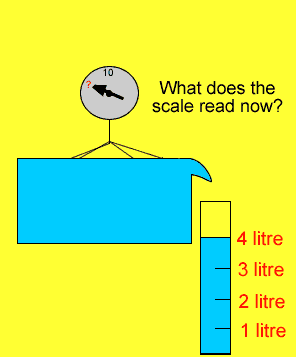
A ten kilogram brick is lowered into a tub of water.

If the density of water is 1g/cm3 what is the reading of the scale when the brick is fully submerged?

Does the brick lose mass when it is placed in water?

Solution

 

 
A brick is dropped into a deep well. The water pressure, indicated by the red arrows, increases with depth. At what depth is the buoyant force acting on the brick at its greatest?
Solution

 

 

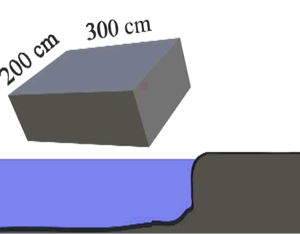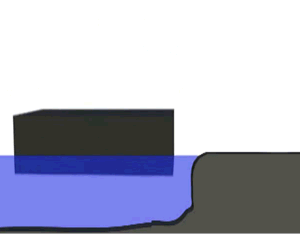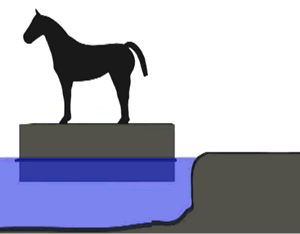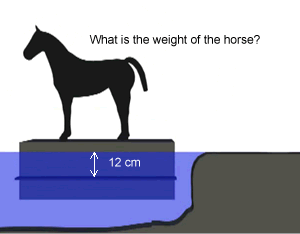
A barge floats on the surface of the water. It's dimensions are shown on the right. A horse jumps onto the barge and the barge is seen to sink a further 12cm.

a) Calculate the volume of the displaced water.
Solution

b) Calculate the weight of the horse.
Solution

Continue with an activity creating a density toy.
Continue with the Cartesian Diver