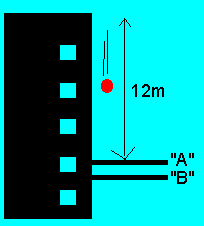
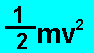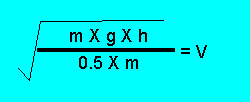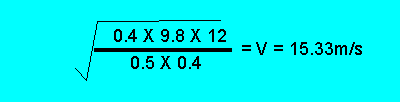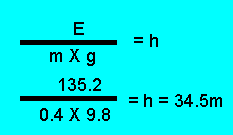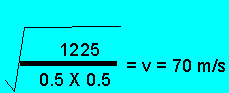A 400 gram ball is dropped onto
two panes of glass as shown on the left. Glass "A will shatter if the
ball hits it with a speed of 20m/s. Glass "B" will also shatter
if the ball hits the first pane of glass at a speed exceeding 26m/s.
The ball is dropped from a height
of 12m onto the first pane of glass. WIll glass "A" shatter?
For glass "A"
to shatter the ball must impact it with a speed of, at least 20m/s. The actual
speed of the ball is 15.33m/s, not enough to shatter the glass. How did we
arrive at this speed?
Step one- The law
of conservation of energy applies. All the gravitational potential energy
is converted into kinetic(moving)energy on impact.
Step two- The gravitational
energy stored by the ball as it sits above the glass is calculated by the
expression below.
E
=mgh
(mass in kilograms,g is the
gravitational constant(9.8), h is the height in metres)
Gravitational potential energy of the ball = 0.4 X 9.8 X 12 = 47.04 joules.
The gravitational potential energy is equal to the kinetic energy on impact.
E
=mgh =
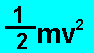
Step 3 - Transform
the formula above to equal "V"
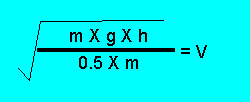
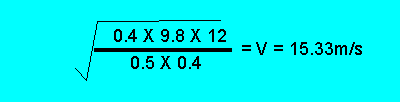
Click
to
hide solution
A 400 gram ball is dropped onto
two panes of glass as shown on the left. Glass "A will shatter if the
ball hits it with a speed of 20m/s. Glass "B" will also shatter
if the ball hits the first pane of glass at a speed exceeding 26m/s.
From what height
above glass "A" must the ball be dropped in order to just shatter
glass "B"? Assume no air resistance.
The law of conservation of energy
applies. The gravitational potential energy of the ball above the glass("A")
will be converted into kinetic energy at the moment of impact with the glass.
The expression below follows.
E
=mgh =
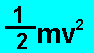
Step 1 -find the kinetic
energy the ball has at the moment of impact with glass "A" assuming
it must have speed of 26m/s.
E
=
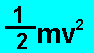
Kinetic energy = 0.5 X 0.4 X 26
X 26 =135.2 joules
Step 2 - Transform
the formula below to make it equal to "h" and then calculate "h"
E
=mgh
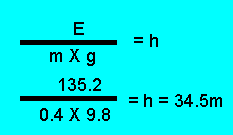
Click
to hide solution
2) Animation shows the different
stages of a rocket launch. The rocket reaches a maximum altitude of 250m.
Assuming no mass loss what is the speed with which the rocket hits the ground?
Step one- The law
of conservation of energy applies. All the gravitational potential energy
of the rocket at maximum altitude is converted into kinetic(moving)energy
on impact.
Step two- The gravitational
energy stored by the rocket as it reaches maximum altitude is calculated by
the expression below.
E
=mgh
(mass in kilograms,g is the
gravitational constant(9.8), h is the height in metres)
Gravitational potential energy of the ball = 0.5 X 9.8 X 250= 1225 joules.
The gravitational potential energy is equal to the kinetic energy on impact.
E
=mgh =
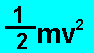
Step 3 - Transform
the formula above to equal "V"
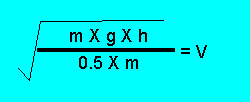
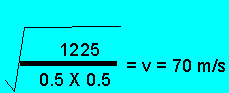
Click
to
hide solution
More kinetic energy exercises

|
|
1)A 400 gram ball is dropped
onto two panes of glass as shown on the left. Glass "A will shatter
if the ball hits it with a speed of 20m/s. Glass "B" will also
shatter if the ball hits the first pane of glass at a speed exceeding
26m/s.
The ball is dropped from a
height of 12m onto the first pane of glass. Will glass "A" shatter?
Assume no air resistance.
Solution
From what height
above the glass "A" must the ball be dropped in order to just
shatter glass "B"? Assume no air resistance.
Solution
|
2) Animation on the right
shows the different stages of a rocket launch. The rocket reaches a
maximum altitude of 250m. Assuming no mass loss, what is the speed with
which the 500g rocket hits the ground?
Solution
|
 |
|
|