Speed is the measure of how fast something is moving. It is the rate at which distance is covered.

We define speed as the distance covered per unit time.

We can use the distance time graph to calculate the speed at a particular interval. The slope of the distance-time graph gives an indication of how fast something is travelling. In fact he slope of the distance-time graph is the speed of the object.

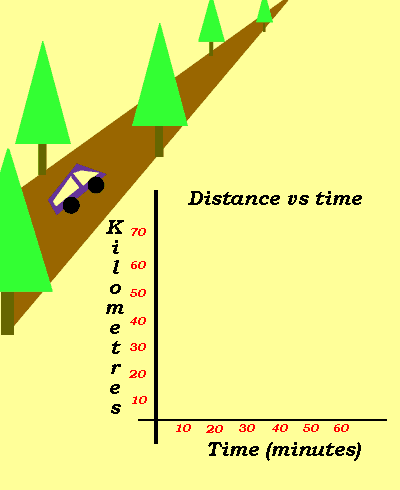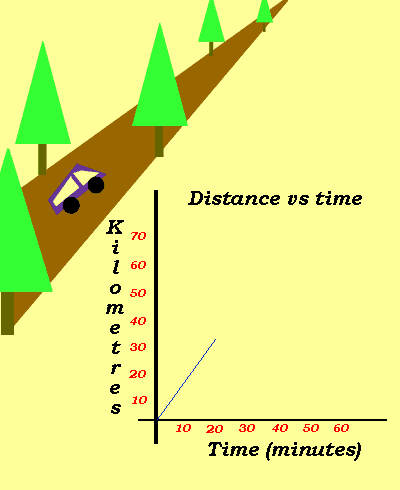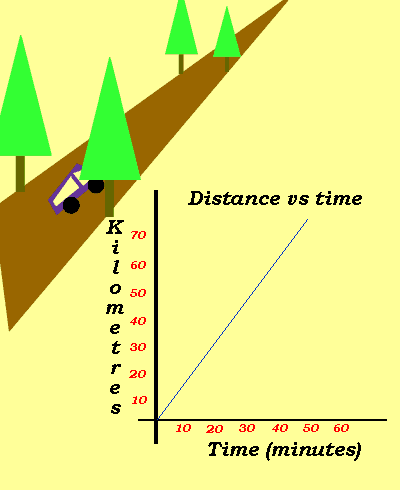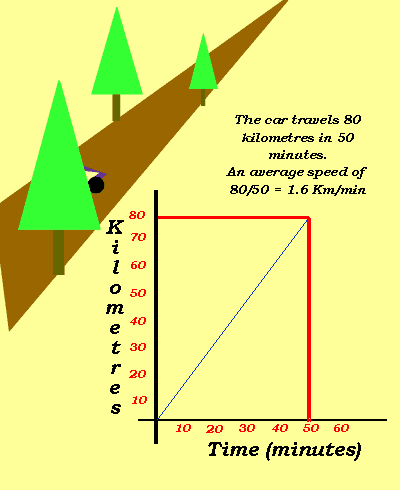
Look at the example on the right. A car travels at a steady speed for 80km in 50 minutes.

The speed of this vehicle can easily be calculated. Simply divide the distance (80km) by the time it took to travel this distance (50min)

Speed =80/50 = 1.6km/min

Now if we wish to get the speed in kilometres per hour we must convert 50 minutes into hours and then divide.

50/60 = 0.83 hours. So the speed in km/hr is
=> 80km/0.83hr = 96.39km/hr

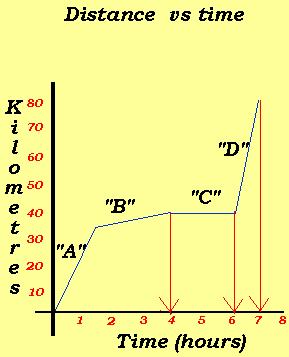
Lets look at the distance-time graph on the left. The slope of the graph indicates the speed of the object.
As one can see section "A" is steeper than section "B" indicating that the speed during section "A" is greater than in "B".
The speed during section "C" is zero because there is no slope. Distance is not changing with time. Section "D" is the steepest indicating that the car is travelling the fastest during this period.

Now the average speed of the car during any interval is given by the expression

So during interval "A" the car travels 35km in 1.5 hours.
The speed over this interval is 35/1.5 = 23.33km/hr.

During interval "B" the car travels 5km in 2.5hrs.
The speed over this interval is 5/2.5 = 2km/hr

During interval "D" the car travels 40km in 1 hr.
The speed over this interval is 40/1 = 40km/hr