The sport of curling depends on the law of inertia and conservation of momentum and collisions.
The law of inertia can be simply stated as "a body in motion will continue in a straight line unless it is acted upon by an outside force" . This is easily demonstrated in curling where the puck will continue to travel in a straight line and at constant speed, since the frictional forces on the ice are minimal. In the absence of external forces the puck will move indefinitely in a straight line.
Inertia can also be applied to a stationary body, in that a stationary body will remain stationary unless acted on by an outside force.

The puck's inertia keeps it moving in a straight line and at a constant speed.
As the puck travels along the ice it has momentum.
Simply put - momentum = mass X velocity.

When the puck collides with another puck on the ice the collision is said to be elastic. To put you in the picture, an elastic collision is one that does not deform the objects colliding and does not generate heat.
In elastic collisions we conserve momentum. That is, the momentum of all of the pucks before the collisions will be exactly the same as the sum of the momentum of of the pucks after the collision.

Let's take a look at what I mean.
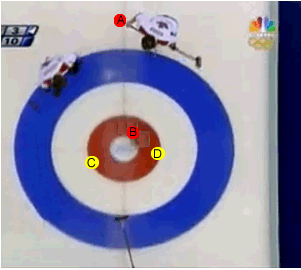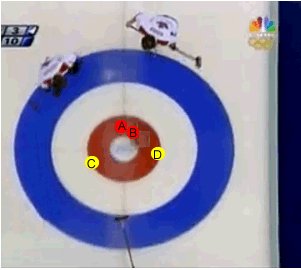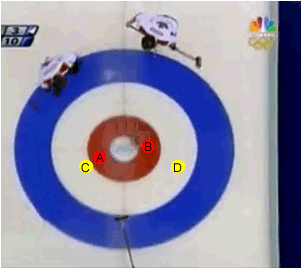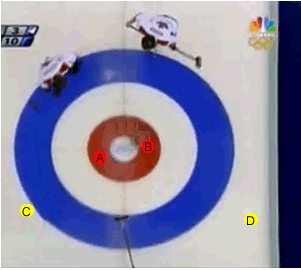
As puck "A" approaches the collision point it has a certain momentum, depending on its speed. It collides with puck "B" which goes on to collide with puck "D". Now puck "A" travels a little slower as it has less momentum after the collision than before. Why is this so if momentum is conserved? Well, this is because puck "B" has taken some momentum from Puck "A" .
Puck "B" now moves on to collide with puck "D" while puck "A" continues on and collides with puck "C". After the collision puck "A" comes to a complete stop as it has transferred all its momentum to puck "C". Puck "B" also comes to a complete stop as it to transfers all its momentum to puck "D".
The sum of the momentum from puck "C" and "D" after the collisions is equal to the momentum of puck "A" before the collisions.
Click to see the elastic collisions of the pucks in a real situation. Exciting isn't it?
3) Puck "A" travels at 2.0 m/s and weighs 13.0 kg.
a) What is the sum of the momentum of puck "A", "B" and "D"?
b) What is the momentum of puck "B" after collision with puck "D"?
c) What happens to the speed of puck "A" after collision?
