Uses for similar triangles.
Introduction to trigonometry
We can take similar triangles a step further especially right angle triangles.
For any right angle triangle we can construct a similar triangle using, something called, the unit circle, shown on the right. This is a circle of radius 1. For every angle between 0 and 360 we have measured sin and cos and often present them in table form or keep them in a calculator.
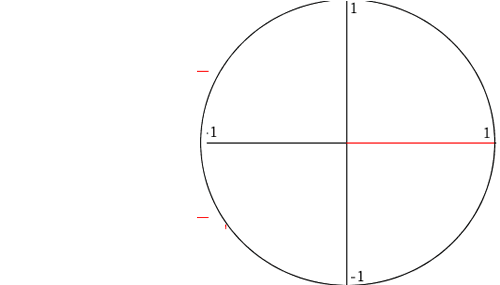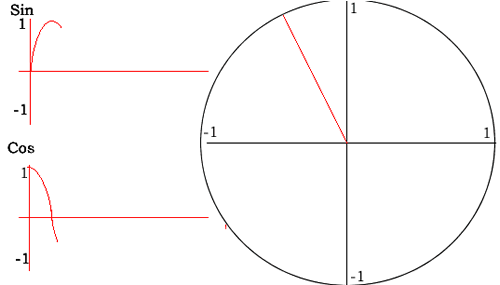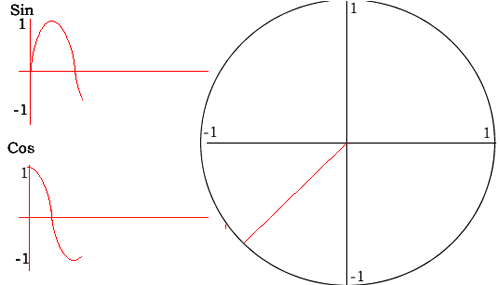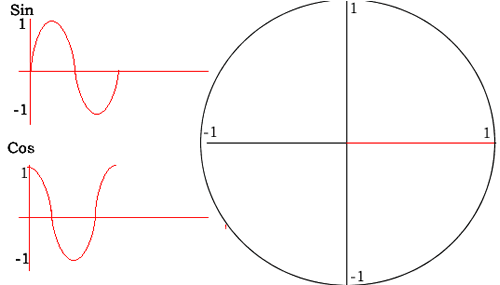
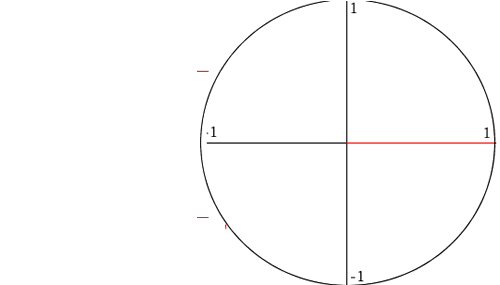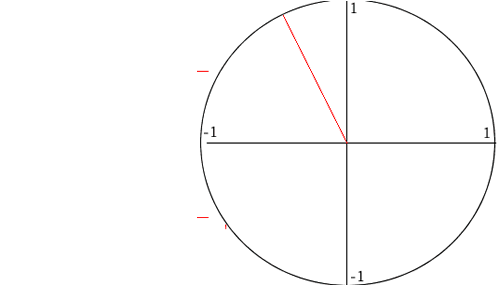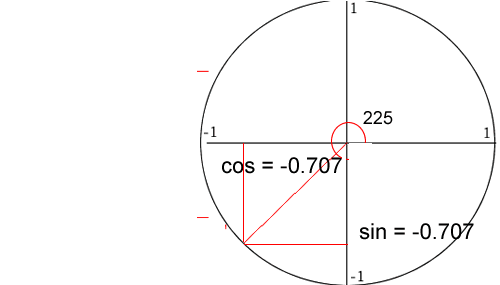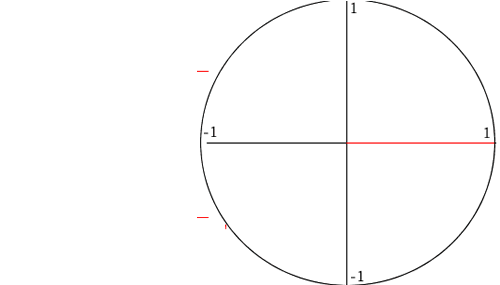
The animation on the right shows how the values of cos and sin are derived for each angle from the unit circle.
At say:
-
30o cos = 0.866 and sin = 0.500.
- 45o cos = 0.707 and sin = 0.707
- 60o cos = 0.500 and sin = 0.866
But how is this trigonometry? Well, trigonometry is the application of the unit circle to every day problems. Lets see how it works.
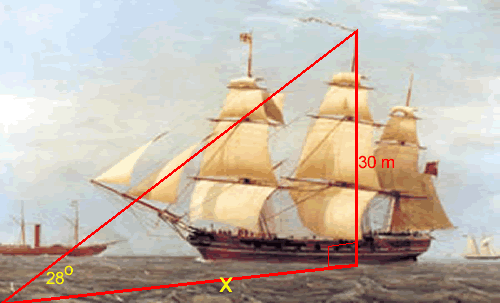
Jonathon observes a ship out at sea. He knows that the highest point on the ship is 30 m above the sea level. He then measures the angle between the sea level and the highest point on the ship as being 28o. How far out at sea is the ship?
Step 1 Construct a similar right angle triangle using the unit circle.
Step 2 Using similar triangles calculate the distance from shore.
Try this one on your own.
A hot air balloon is tethered to the ground by a 120m long rope. It is allowed to rise and the rope becomes tight making an angle of 30o with the ground.
Click to see the animation if you need to..
The sin of 30o is 0.500 and the cos of 30o is 0.866
How high off the ground is the balloon?
Need help?
Step 1 Construct your similar right angle triangle using the unit circle.
Step 2 Using similar triangles calculate the height

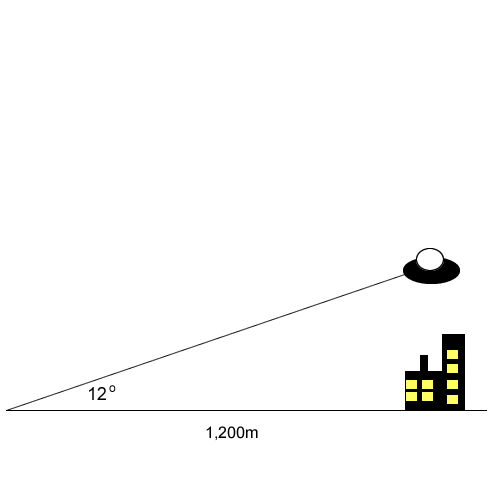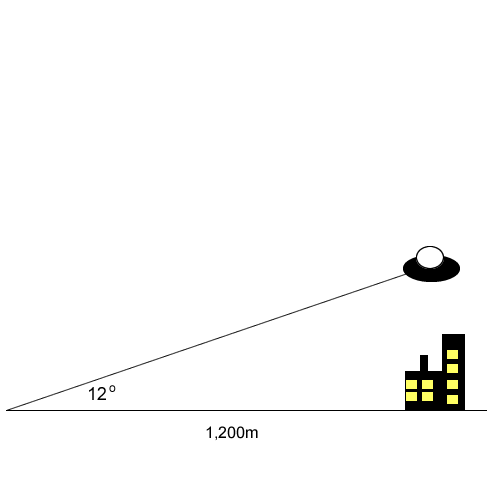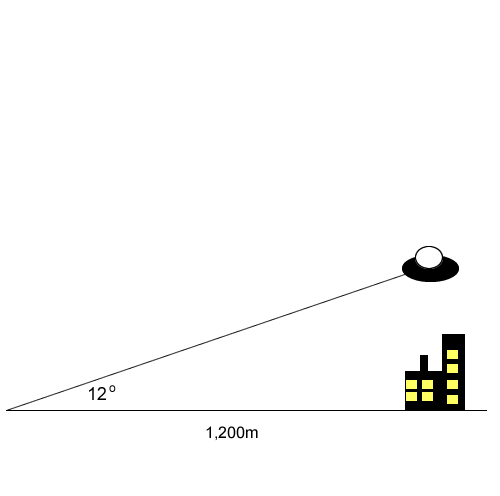
A laser beam is pointed at a UFO hovering above a city 1,200m away. The laser beam makes an angle of 12o with the ground, as shown on the right.
How far above the ground is the UFO?
Use the tables for sin and cos values.
Click to view the problem again.
Need help?
Step 1 Construct your similar right angle triangle using the unit circle.
Step 2 Using similar triangles calculate the height
Now this one is totally yours to do without any help.
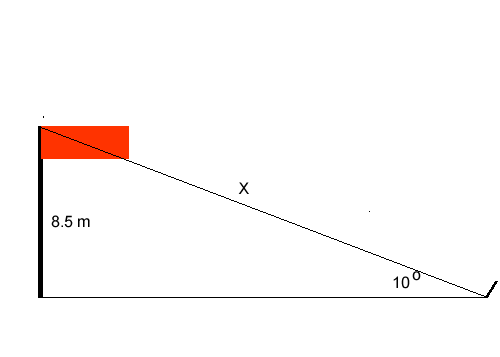
An 8.5m flag pole is supported by a wire tied to the top of the flag pole and to a stake in the ground. If the wire makes an angle of 10o with the ground how long is the wire?
Solution
A ship heads off in a straight course on a bearing S35oW for a distance of 800 kilometres. How far South has it travelled?
The sin 35o = 0.574 and cos 35o = 0.819
The sin 55o = 0.819 and cos 55o = 0.574
Step 1 Sketch the problem and create the appropriate right angle triangle.
Step 2 Construct your similar right angle triangle using the unit circle.
Step 3 Using similar triangles calculate the distance South.
