flight- energy gravitational potential exercises

Solution

mgh = 120 X 9.8 X 150 = 176400 joules

=176.4 kilojoules

Hide the solution

Solution

The car originally has gravitational potential energy of
mgh = 0.05 X 9.8 X 50
=24.5 joules of energy
When it descends to point "B" the gravitational potential energy is
mgh = 0.05 X 9.8 X 30
=14.7 joules.
The amount of energy lost is
= 24.5 -14.7 =9.8joules

Click to hide the solution

Solution

The gravitational potential energy is given by the formula
mgh

The mass at peak altitude is 120.00 - 47.67 = 72.33g.
So

mgh = 0.07233 X 9.8 X 100 = 70.88 joules.

Hide solution

Solution

The mass of the plane at the point where there is no more fuel is
2,349 - 459 -359 = total mass of the plane and pilot. =1531kg

As the plane descends 10m every second it will descend 600m every minute. The gravitational potential energy the plane losses every minute is calculated by the expression

mgh = 1531 X 9.8 X 600 = 9002.3kilojoules/minute

If the plane descends 600m every minute then it will take

27300/600 = 45.5 minutes

Hide the solution

Gravitational potential energy exercises
An 120kg firefighter is trapped on top of a burning building. Her colleagues on the ground suggest she jump. Calculate the firefighter's gravitational potential energy content if the top of the builing is 150m high. Solution
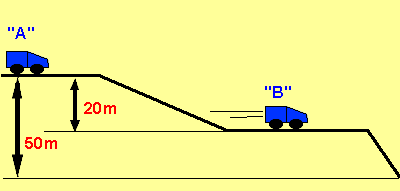
	A 50g toy car slowly descends from a height of 50m by coming down a set of ramps. Calculate the amount of gravitational potential energy the vehicle has lost as it descends from point "A" to point "B". Assume no friction or air resistance. Solution
A 120g model rocket sits on the launch pad ready for launch. It contains 47.67g of fuel. The rocket reaches a peak altitude of 100m. Assuming all the fuel is burnt, calculate the gravitational potential energy of the rocket at peak altitude. Solution
	A plane with a total mass of 2,349kg (incudes 459kg of fuel) is flying at a constant altitude of 2.73km above the ground. A 359kg payload is dropped from the plane when the pilot realises she has no more fuel. The plane glides for a while dropping 10m per second. Calculate the loss of gravitational potential energy every minute. How long will it take for the plane to land? Solution
Continue