Physics-component vectors

Click to hide the solution

A cannon ball is fired skywards with an unknown initial vertical velocity and an initial horizontal velocity of 4 m/s as shown on the right. Ignore air resistance
g=10 m/s/s

a) How long does the ball take to reach its maximum height? (use the formula
d =(1/2)gt²
b) What is the initial vertical velocity of the ball?
c) What is the velocity of the ball just before impact at "B"?
d) How far is point "B" from the launch site?

a) How long does the ball take to reach its maximum height? (use the formula
d =(1/2)gt²

200 = (1/2)10t^{2

=> 40 =}t²
=> 6.32s = t

b) What is the initial vertical velocity of the ball?
v =d/t
=>v = 200/6.32
=>v = 31.65 m/s

c) What is the velocity of the ball just before impact at "B"?
The velocity at impact is equal in magnitude but opposite in sign to the initial velocity.
The magnitude of the initial velocity is obtained by adding the vertical and horizontal velocity vectors. Using the Pythagorean Theorem we obtain a value of 31.90 m/s

d) How far is point "B" from the launch site?
To work out the horizontal distance we must use the horizontal velocity. The ball is in the air for 12.64 seconds. So using hte formula d=vt
distance = 4 m/s X 12.64s = 50.56 m.

Click to hide the solution

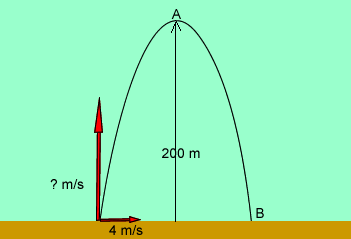
Remember that the horizontal and vertical velocities are independent of each other.

To work out the horizontal velocity we use the formula d/t. Now d = 400m and t = ?
To calculate t we use the formula d = 0.5gt^{2

=> 400 = 0.5 X 10 X t²

=> 80 = t²

=> 8.94s = t

So a vertical distance of 400m must be covered in 8.94s. The vertical velocity
must be

v = 400/8.94 = 44.74 m/s.}

^{To calculate
the horizontal velocity again we use the formula v = d/t.

Now d =600 and t = (2 X 8.94) = 17.88s.

So v = d/t

=>v = 600m/17.88s

=>v = 33.56 m/s}

As the cannon ball passes over the peak its vertical velocity has shrunk to zero. It only has horizontal velocity so it passes at a speed of 33.56 m/s

The cannon ball will strike the target at a speed equivalent to its initial speed. We calculate the initial speed by working out the magnitude of the resultant initial velocity vector.
We use Pythagorean Theorem
s² = (hv)² + (vv)² Where s =magnitude of initial velocity vector, hv = initial horizontal velocity and vv = initial vertical velocity.
=> s² = (33.56)² + (44.74)^{2

=> s = 55.93 m/s}

Component vectors
Any vector quantity can be resolved into two componenet vectors at right angles to each other. Look at the animation on the right. The process where by a vector is separated into its component vectors is called resolution. Any vector drawn on paper can be resolved into its vertical and horizontal components.
Knowing that the velocity vector drawn above is to scale and that its magnitude is 360 km/hr, we can calculate the magnitude of the component vectors. The scale appears to be 360km/hr/3.6cm = 100km/hr/cm. So every cm represents 100km/hr. So the vertical component is 2 cm in length and has a magnitude of 200 km/hr, while the horizontal component is 3 cm in length and has a magnitude of 300 km/hr.
Using a ruler resolve the velocity vector shown on the right. If the magnitude of this vector is 144.2 km/hr find the magnitude of the component vectors.
Using a ruler resolve the velocity vector shown on the right. If the magnitude of this vector is 123.69 km/hr find the magnitude of the component vectors.
Using a ruler resolve the velocity vector shown on the right. If the magnitude of this vector is 47.17 km/hr find the magnitude of the component vectors.
Using a ruler resolve the velocity vector shown on the right. If the magnitude of this vector is 42 km/hr find the magnitude of the component vectors.
Direction of vectors