Resultant vectors
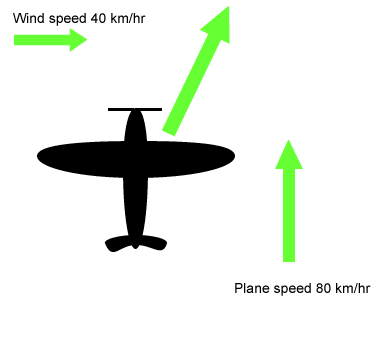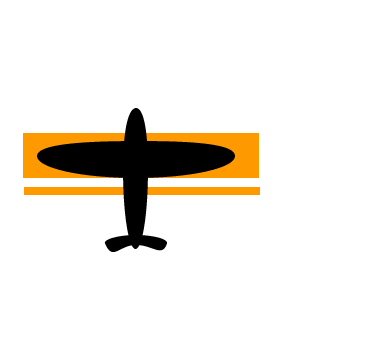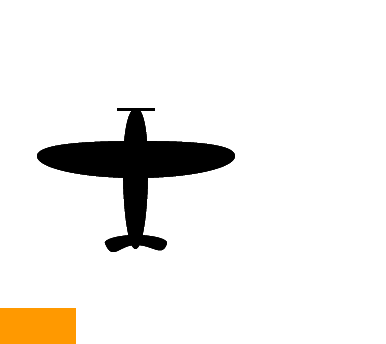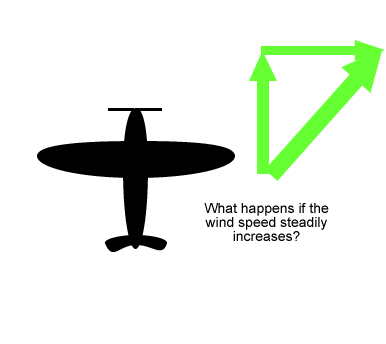
Consider our plane flying at a speed of 80 km/hr into a 40 km/hr crosswind. Its speed, relative to the ground, can be calculated by adding the two vectors as shown on the right. What happens to the speed of the plane as the crosswind increases in magnitude? Look at the animation on the right. It is obvious that the speed of the plane, relative to the ground, increases in magnitude.

How do we calculate the magnitude of the resultant vector? Whenever a pair of vectors are at right angles to each other we can use the Pythagorean Theorem to calculate the magnitude of the resultant vector.

A plane travels at a speed of 80 km/hr east and encounters a 20 km/hr cross wind. What is the speed of the plane relative to the ground?

Once again have a look at the animation on the right.


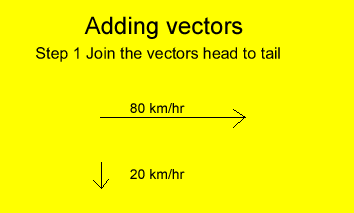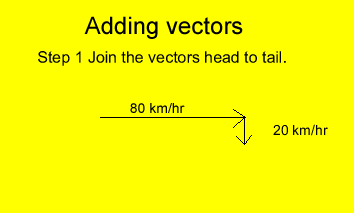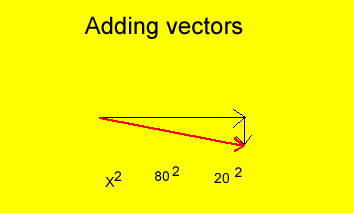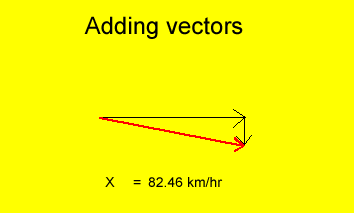
Image from Google

1) A surfer rides along a wave traveling towards the shore at 30 km/hr. The surfer rides along the wave at 40 km/hr parallel to the shore. With what speed is the surfer traveling relative to the shore?

Solution

A plane travels south at 40 km/hr. A 20 km/hr westerly wind is acting on the plane. What is the speed of the plane relative to the ground? Solution

An athlete attempting a long jumps runs down the track at 40km/hr before launching himself vertically into the air. What is his speed in the air if he launches himself with a vertical velocity of 20 km/hr? Solution

A plane traveling west at 40 km/hr encounters a wind blowing south at 40 km/hr.
What is the speed of the plane relative to the ground?
In what direction is the plane now traveling?
Solution

Calculate the resultant of a pair of velocities 80 km/hr north and 60 km/hr west.
Solution

Calculate the magnitude of the resultant of a horizontal vector with a magnitude of 5 units and a vertical vector with a magnitude of 3 units.
Solution

Neglecting air resistance, a bullet leaves the barrel of a gun with a velocity of 400km/hr. It strikes a target 600m away. Will the bullet strike the target with a velocity of 400 km/hr, less or greater than 400 km/hr?

Image from Google

The term "Hang time" is used in athletics to describe the length of time an athlete can jump off the ground. In sports such as long-jump hang time is critical. The longer the hang time the greater the distance that the athlete can jump.

At the point the athlete leaves the ground they have a resultant velocity composed of horizontal and vertical velocities at right angles to each other.

Hang time depends on the vertical or horizontal velocity?

Distance traveled depends on the horizontal or vertical velocity?

Why do athletes seek to increase their horizontal velocity by sprinting down the track before jumping? Solution

A construction worker walks across a beam. The beam bends to support the person's weight. The downward force applied by the person on the beam is equal and opposite to the force applied by the beam on the person. Why must the beam bend in order to support the person? Solution.
Think of:
- tensile force generated in the beam.
- component vectors

Component vectors

Continue with projectile motion