Vectors
To completely describe
a vector we need to know its magnitude and direction. A scalar quantity
can be completely described by its magnitude only. Scalar quantities
can be added, divided, subtracted and multiplied like any other value.
For example
2 kg of sugar is a scalar quantity. When we mix 4 kg of sugar and 5
kg of salt the mixture has a mass of 9 kg.
Speed is also a scalar value as is time and volume.
Velocity is a vector quantity because it can be completely described when its magnitude and direction are known.
Consider a plane flying west at 80 km/hr. Suppose it encounters a wind blowing south at 20 km/hr. This situation is represented by vectors "A" and "B" on the right. Here the velocity vectors are scaled so that 1 cm is equivalent to 20 km/hr.
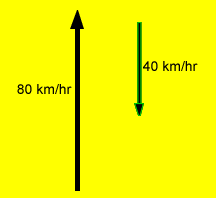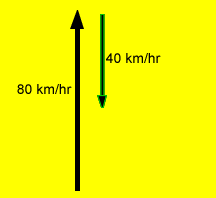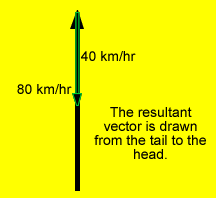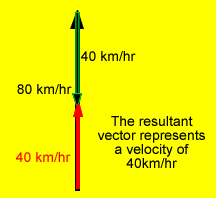
The plane now flies into a 40 km/hr head wind represented by vector "C".
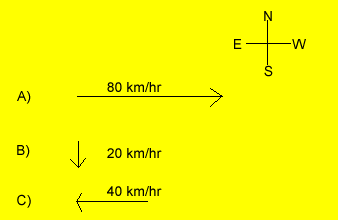
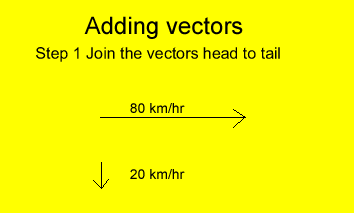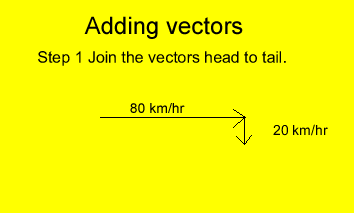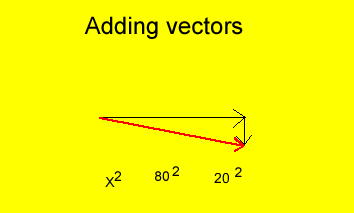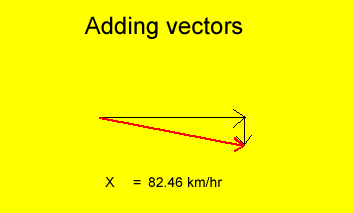
Suppose that the plane discussed above traveling at 80 km/hr encounters a 20 km/hr crosswind. Will the plane fly faster or slower than 80 km/hr?
To answer this question we have to add the two vectors, namely the velocity of the plane and the velocity of the crosswind.
Follow the animation on the right.
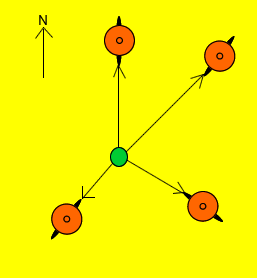
In all our examples we have used only two vectors, but we can add an infinite number of vectors. Consider the problem shown on the right. Four Mexican cyclists pull on a rope tied to a ball. The vectors represent the force with which each cyclist pulls on the rope. In which direction will the ball travel?
Once again you add the vectors by placing them head to tail.